Use the DELAY builtins to delay the input by a delay duration, or to exponentially smooth the input over an averaging time.
This section describes the following builtins:
The DELAY builtin returns a delayed value of input, using a fixed lag time of delay duration, and an optional initial value initial for the delay. If you don't specify an initial value initial, DELAY assumes the value to be the initial value of input. If you specify delay duration as a variable, the DELAY function uses the initial value for its fixed lag time.
Example:
Shipments = DELAY(Orders,5) will cause shipments to lag behind orders by 5 time units. For the first 5 time units of the simulation, the delay will return the initial value for orders - since no initial value was specified.
The DELAY1 builtin calculates a first-order material delay of input, using an exponential delay time of delay duration, and an optional initial value initial for the delay. If you don't specify an initial value, DELAY1 assumes the value to be the initial value of input.
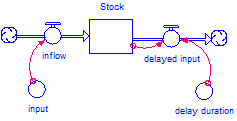
The DELAY1 builtin is equivalent to the structure and equations shown in the following figure. This structure is a draining process.

Stock = Stock + DT*(inflow - delayed_input)
INIT Stock = input*duration_delay or specified initial value*duration_delay
inflow = input
delayed_input = Stock/delay_duration
input = some variable or constant
delay_duration = some variable or constant
Example:
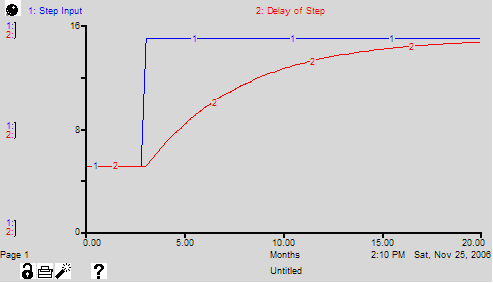
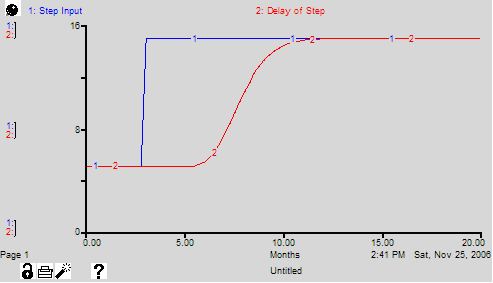
Delay_of_Step = DELAY1(Step_Input, 5) where Step_Input = 5 + STEP(10,3) produces the pattern shown in the following graph.
Note: The dynamic behavior of DELAY1 is identical to SMTH1, except when the delay time changes. In this case, DELAY1 conserves material while SMTH1 doesn't. DELAY1 is conceptually a flow, and SMTH1 is conceptually a stock. Because DELAY1 is a flow concept, you must C-to-F any converter that uses this function, if you want to see the correct reported results in a table (or when exported).
The DELAY3 builtin calculates a third-order material delay of input, using an exponential delay time of delay duration, and an optional initial value initial for the delay. DELAY3 does this by setting up a cascade of three first-order material delays, each with a delay duration of delay duration/3. DELAY3 returns the value of the final delay in the cascade. If you don't specify an initial value, DELAY3 assumes the value to be the initial value of input.
The DELAY3 builtin returns the value of 'delay 3' in the structure and equations shown in the following figure.
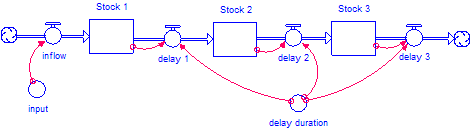
INIT Stock_1 = INIT Stock_2 = INIT Stock_3 = input or specified initial value times duration_delay/3
inflow = input
delay_1 = Stock_1/(delay_duration/3)
delay_2 = Stock_2/(delay_duration/3)
delay_3 = Stock_3/(delay_duration/3)
input = some variable or constant
delay_duration = some variable or constant
Example:
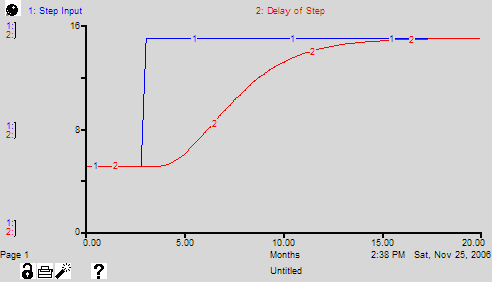
Delay_of_Step = DELAY3(Step_Input, 5) where Step_Input = 5 + STEP(10,3) produces the pattern shown in the following graph.
Note: The dynamic behavior of DELAY3 is identical to SMTH3, except when the delay time changes. In this case, DELAY3 conserves material while SMTH3 doesn't. DELAY3 is conceptually a flow, and SMTH3 is conceptually a stock. Because DELAY3 is a flow concept, you must C-to-F any converter that uses this function, if you want to see the correct reported results in a table (or when exported).
The DELAYN builtin calculates an nth-order material delay of input, using an exponential delay time of delay duration, an order number of n, and an optional initial value initial for the delay. DELAYN does this by setting up a cascade of n first-order material delays, each with a delay duration of delay duration/n. DELAYN returns the value of the final delay in the cascade. If you don't specify an initial value, DELAYN assumes the value to be the initial value of input. The value of n should be specified as an integer, and must be between 1 and 255 (and will be truncated silently if it's not).
Example:
Delay_of_Step = DELAYN(Step_Input, 5, 9) where Step_Input = 5 + STEP(10,3) produces the pattern shown the following graph.
Note: The dynamic behavior of DELAYN is identical to SMTHN, except when the delay time changes. In this case, DELAYN conserves material while SMTHN doesn't. DELAYN is conceptually a flow, and SMTHN is conceptually a stock. Because DELAYN is a flow concept, you must C-to-F any converter that uses this function, if you want to see the correct reported results in a table (or when exported).
Note: If n is large, and the time delay is small, the intermediate transition times between the stocks can become smaller than DT. To prevent unstable behavior in this situation, the length of the delay will be increased to n*DT. Normally, n should be much smaller than delay_duration/DT.
The SMTH1 builtin calculates a first-order exponential smooth of input, using an exponential averaging time of averaging time, and an optional initial value initial for the smooth. If you don't specify an initial value, SMTH1 assumes the value to be the initial value of input.
The SMTH1 builtin is equivalent to the structure and equations shown in the following illustration.
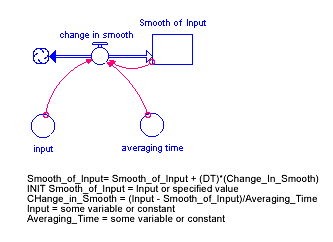
This structure is a stock-adjustment process. Smooth of Input seeks the goal Input.
Example:
Smooth_of_Step = SMTH1(Step_Input,5)
where
Step_Input = 5 + STEP(10,3) produces the pattern shown in the following graph.
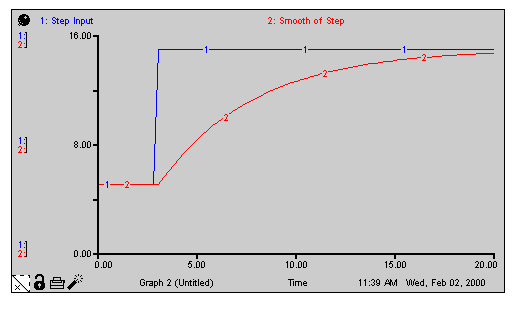
Note: The dynamic behavior of SMTH1 is identical to DELAY1, except when the averaging time changes. SMTH1 is conceptually a stock, and DELAY1 is conceptually a flow.
The SMTH3 builtin performs a third-order exponential smooth of input, using an exponential averaging time of averaging time, and an optional initial value initial for the smooth. SMTH3 does this by setting up a cascade of three first-order exponential smooths, each with an averaging time of averaging time/3. SMTH3 returns the value of the final smooth in the cascade. If you don't specify an initial value, SMTH3 assumes the value to be the initial value of input.
The SMTH3 builtin returns the value of Stock 3 in the structure and equations shown in the following illustration.
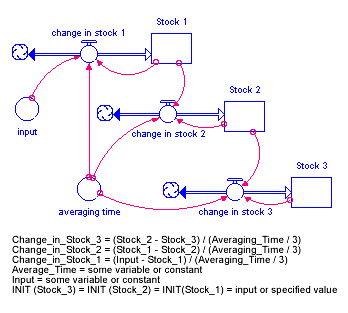
Examples:
Smooth_of_Step = SMTH3(Step_Input,5)
where
Step_Input = 5 + STEP(10,3) produces the pattern shown in the following graph.
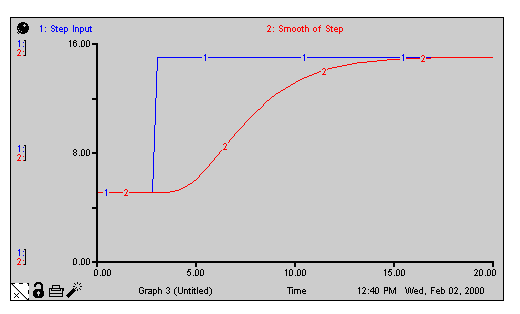
Note: The dynamic behavior of SMTH3 is identical to DELAY3, except when the averaging time changes. SMTH3 is conceptually a stock, and DELAY3 is conceptually a flow.
The SMTHN builtin performs an nth-order exponential smooth of input, using an exponential averaging time of averaging time, an order number of n, and an optional initial value initial for the smooth. SMTHN does this by setting up a cascade of n first-order exponential smooths, each with an averaging time of averaging time/n. SMTHN returns the value of the final smooth in the cascade. If you don't specify an initial value, SMTHN assumes the value to be the initial value of input. The value of n should be specified as an integer between 1 and 255 (and will be truncated silently if it's outside this range).
Examples:
Smooth_of_Step = SMTHN(Step_Input,5,9)
where
Step_Input = 5 + STEP(10,3) produces the pattern shown in the following graph.
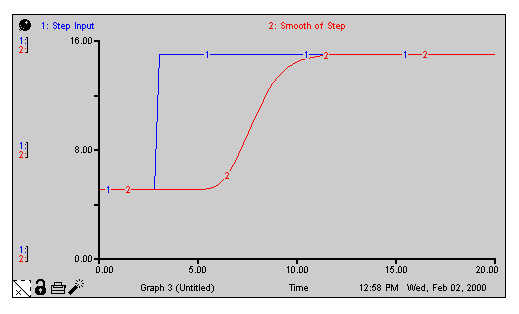
Note: The dynamic behavior of SMTHN is identical to DELAYN, except when the averaging time changes. SMTHN is conceptually a stock, and DELAYN is conceptually a flow.
Note: If n is large, and the time delay is small, the intermediate transition times between the stocks can become smaller than DT. To prevent unstable behavior in this situation, the length of the delay will be increased to n*DT. Normally, n should be much smaller than delay_duration/DT.