The Runge-Kutta method
It's always possible to reduce integration error by making the
DT of your models smaller. As DT approaches zero, Euler's approximation
approaches the exact solution. But as you make DT smaller, you also increase
the number of calculations (and the time) required to conduct your simulation, and eventually introduce significant rounding errors
- clearly not a desirable outcome. Another way to reduce the integration
error is to use a more sophisticated procedure for estimating the change
in stocks over a given DT; the Runge-Kutta algorithm gives you a higher
degree of accuracy.
Note Because Runge-Kutta integration includes computations between values of DT, not all computed values of variables can be reported. There is an option in the Model Settings Properties Panel to adjust flows so that their reporting in tables will represent the average value across computations rather than the value directly on the current DT.
To aid in the exposition of Runge-Kutta, a bit of notation will prove
helpful. Let "x" represent
any stock and "f(t,x)" represent
the functional notation for flows that depend on time "t" and stock "x".
2nd-order Runge-Kutta
Of the two Runge-Kutta methods, 2nd-order is the simpler. Basically, this algorithm uses two flow calculations within a given DT to create an estimate for the change in a stock over the DT. As with Euler's method, the solution of equations involves both an initialization and an iteration phase.
Initialization Phase (Runge-Kutta 2)
Step 1. Create a list of all stocks, flows, and converters, in required order of evaluation.
Step 2. Calculate initial values of all stocks, flows, and converters (in order of evaluation).
Time = From Time
Stockt=0 = f(initial values, stocks, converters, flows)
Converters = f(stocks, converters, flows)
Flows = f(stocks, converters, flows)
Iteration Phase (Runge-Kutta 2)
Step 1.
(a) Estimate change in stocks over the interval DT. Use two points to create this estimate:
(1) F1 = dt * f(t, x) [the same as Euler's flow estimate]
(2) F2 = dt * f(t+dt, x + F1)
(3) stock = 1/2 * (F1 + F2)
(b) Calculate new value for stocks based on this estimate.
Stockt = Stockt-dt + stock
Step 2. Calculate new values for flows and converters (in order of evaluation).
Converters = f(stocks, converters, flows)
Flows = f(stocks, converters, flows)
Step 3. Update simulation time. Stop iteration when Time is >= simulation To Time.
Time = Time + dt
The intermediate calculations in Step 1 of the iteration phase enable the 2nd-order Runge-Kutta method to create a more accurate estimate for the change in stocks during a given DT. This estimate is based on an average of flow values computed at the beginning, and at the end, of the DT interval.
4th-order Runge-Kutta
4th-order Runge-Kutta uses four flow calculations (as contrasted with Euler's one calculation) within a given DT
to create an estimate for the change in a stock over the DT. A weighted
average of these calculations is used as the estimate for the change in
the stock. As with Euler's method,
the solution of equations involves both an initialization and an iteration
phase.
Initialization Phase (Runge-Kutta 4)
Step 1. Create a list of all
stocks, flows, and converters, in required order of evaluation.
Step 2. Calculate initial values
of all stocks, flows, and converters (in order of evaluation).
Time = From Time
Stockt=0 = f(initial values, stocks, converters, flows)
Converters = f(stocks, converters, flows)
Flows = f(stocks, converters, flows)
Iteration Phase (Runge-Kutta 4)
Step 1.
(a) Estimate change in stocks over the interval
DT. Use four points to create this estimate:
(1) F1 = dt * f(t,x)
(2) F2 = dt * f(t+dt/2, x + 1/2F1)
(2) F3 = dt * f(t+dt/2, x + 1/2F2)
(4) F4 = dt * f(t+dt, x + F3)
(5) 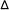 stock = 1/6 * (F1 + 2F2 + 2F3 + F4)
stock = 1/6 * (F1 + 2F2 + 2F3 + F4)
(b) Calculate new value for Stocks based
on this estimate.
Stockt = Stockt-dt + 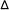 stock
stock
Step 2. Calculate new values
for flows and converters (in order of evaluation).
Converters = f(stocks, converters, flows)
Flows = f(stocks, converters, flows)
Step 3. Update simulation time.
Stop iteration when Time is >= simulation To Time.
Time = Time + dt
The intermediate calculations in the first step of the iteration phase
are the key to the 4th-order Runge-Kutta method. F1
represents the rate of change of the stock, i.e., the flow, at time "t".
F2 is a new calculation of the flow, at
1/2 an interval into the future, t+dt/2.
In order to calculate F2, F1 is used to
update the stocks. These are then used to re-calculate the flows at t+dt/2. One-half of F1
is used in estimating F2, since the calculation
is made over only 1/2 the interval. F3
is a new calculation of the flow at t+dt/2.
To calculate F3, F2
is used to update the stocks, which are then used to re-calculate the
flows at t+dt/2. Again, only 1/2 of F2 is used to update the stocks, since the
calculation is made over 1/2 an interval. F4
is a calculation of the flow at one full interval in the future, t+dt. To calculate F4, F3is used as the flow over the full interval. The stocks are updated
using F3, then F4
is estimated.
Finally, the four intermediate flow calculations are averaged together,
yielding an estimate of the flow. It's this average flow that's used
to update the stock before the next iteration begins.
 See Also
See Also
stock = 1/6 * (F1 + 2F2 + 2F3 + F4)
stock